
Rotational Motion Name:________________________ Course:________
A. Moment of Inertia
Purpose: Determine the moment of inertia of regularly shaped objects, a disk and a ring, using the Rotary Motion Sensor.
Apparatus: Rotary motion sensor with step pulley, super pulley, lab stand, gray disk, black ring, vernier caliper, thread, mass set, mass hangers, 20-g mass, meter stick, knife-edge support, knife-edge clamp, interface, and PC.
Theory: A hanging mass of 20-g will be used to rotate the disk. As the 20-g mass goes down with a linear acceleration, a the disk will move with an angular acceleration of α. Linear acceleration is given by, a = rα. An expression for the experimental moment of inertia, IE is obtained as follows.

Applying Newton second law for the 20-g mass will yield----> mg - T = ma-------(I)
Applying Newton's second law for the disk will yield--------> T.r = IE α = IE (a/r)------(II)
Eliminating T from the above two equations will yield--------> IE = mr2 (g/a - 1).
Procedure:
1. Find the mass of the gray disk using an electronic balance and the mass of the black ring using torque.
2. Find the dimensions of the ring & disk using the vernier caliper. Check your measurements with the instructor.
3. Connect the rotary motion sensor to the 750 interface by inserting the yellow plug into digital channel-1 and the black plug into digital channel-2.
4. Mount the Rotary Sensor onto the support rod so that the step pulley is on top. Clamp-on the Super Pulley on the end of the sensor (end where the cord is) as shown above.
5. Cut a piece of thread, about 50cm in length. Tie one end to the outer step pulley and the other to a 20-g mass and hang it over the super pulley.
6. Open Data Studio, click Open Activity, double-click Library, double-click Physics Labs, double-click Experiment P22 (Rotational Inertia). Double-click Velocity Graph under Displays.
7. Turn the step-pulley clockwise so that the thread winds around the outer groove of the step pulley and hold it.
8. Click "Start" and release the step-pulley. Stop the data collection.
9. High-light the linear portion of the graph, and click the fit button, and do a linear fit. Obtain the slope which is the acceleration, a. Record a in the data table.
10. Remove the thumb screw and attach the gray disk into the top of the step-pulley. Re-attach the thumb screw.
11. Repeat procedures 7-9.
12. Place the black ring on top of the disk, and repeat procedures 7-9.
13. Calculate the experimental moment of inertia, IE, and the theoretical moment of inertia, IT and complete data table III.
DATA
Table I: Mass of the gray disk = M = _________
Mass of black ring, M1 using torque.
| Unknown mass | Known mass | Lever-arm for known mass | Lever-arm for the unknown mass | Value of the unknown Mass (g) |
| Black ring, M1 | M1 = |
Table II: Dimensions of the step pulley, ring & disk
| Diameter (cm) | Radius (cm) | |
| Step pulley (outer) | 4.76 | r = 2.38 |
| Inside of black ring | R1 = | |
| Outside of black ring | R2 = | |
| Gray disk | R = |
The hanging mass, m = 20-g and the outer step pulley radius, r = 2.38 cm can be used to re-write IE as follows. This expression will be used to calculate IE in Table III, below.
IE = mr2 [(g/a) - 1] = 113 [(g/a) -
1].
Table III:
| Acceleration, a (m/s2) | IE, Experimental*(g.cm2) | IT, Theory**(g.cm2) | % Difference | |
| Pulley alone | XXXXXXXXXXXXX | XXXXXXXXXX | ||
| Pulley & Disk | XXXXXXXXXXXXX | XXXXXXXXXX | ||
| Disk | XXXXXXXX | |||
| Pulley, Disk & Ring | XXXXXXXXXXXXX | XXXXXXXXXX | ||
| Ring | XXXXXXXX |
**IT (disk) = 0.5
MR2; **IT (Ring) = 0.5
M1(R12 +R22
).
*IE, for the disk is obtained by
subtracting the pulley alone value from the pulley & disk
value.
B. Conservation of Angular Momentum
Purpose: Verify the conservation of angular momentum using the Rotary Motion Sensor.
Apparatus: Rotary motion sensor with step pulley, gray disks, interface, and PC.
Theory: In this part you will rotate a disk attached to the rotary motion sensor and let the PC collect the data. While the first disk rotates, a second disk will be dropped onto the first disk. The PC will continue to collect the data. From the display the initial and final angular velocities can be obtained. In this case, there is no net torque, and hence the angular momentum should be conserved.
Conservation of angular momentum gives------->
Iiωi =
Ifωf
The initial
and final moments of inertia can be obtained from Part A.
Procedure:
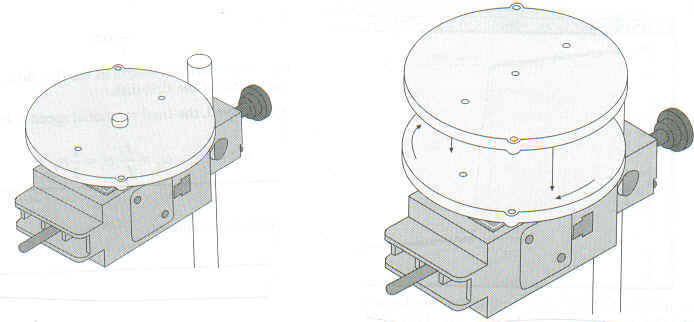
1. The rotary motion sensor is connected to the interface. Remove the black ring and gray disk. Remove the super pulley and the string from the rotary motion sensor.
2. Screw in the gray disk onto the rotary motion sensor.
3. Open Data Studio, click Open Activity, double-click Library, double-click Physics Labs, double-click Experiment P23 (Angular Momentum). Double-click the Angular Velocity Graph under Displays.
4. Spin the gray disk counter-clockwise, then click start.
5.
6. To determine the initial and final angular speeds, use the Smart Tool found on tool bar. Drag the pointer to the data entry that was recorded just before the second disk was dropped. The Y coordinate is the angular speed. The final angular speed is found in the same fashion, this time dragging the Smart Tool to the data entry just after the second disk was dropped. Record both angular speeds.
7. Repeat steps 4 -6, 2 more times and complete the data table.
DATA (Include units)
| ωi | ωf | I i | I f | Li = Iiωi | Lf = Ifωf | % Difference |