Name:_____________________________________ Date: ________Time:__________

Partner(s):_________________________________ ______________________________

                            The Ballistic Pendulum and Projectile Motion

Purpose: To determine the initial velocity (u) of a projectile

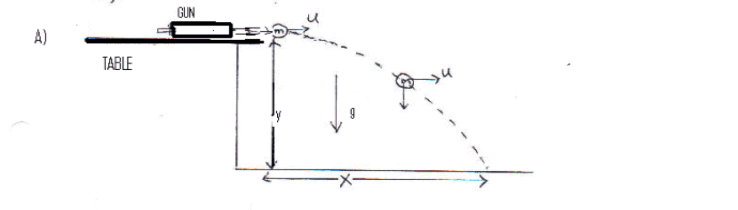
A) by measuring its range and vertical distance of fall

B) by using the conservation of energy and momentum.

Apparatus: ballistic pendulum, meter stick, white paper, carbon paper, tape, balance,

small ruler.

Theory:

By looking at the motion in the vertical direction, derive an expression for the time of flight, t in terms of Y, vertical distance of fall and g, acceleration due to gravity.

 By looking at the motion in the horizontal direction, derive an expression for u, initial horizontal velocity of the projectile, in terms of X and t.

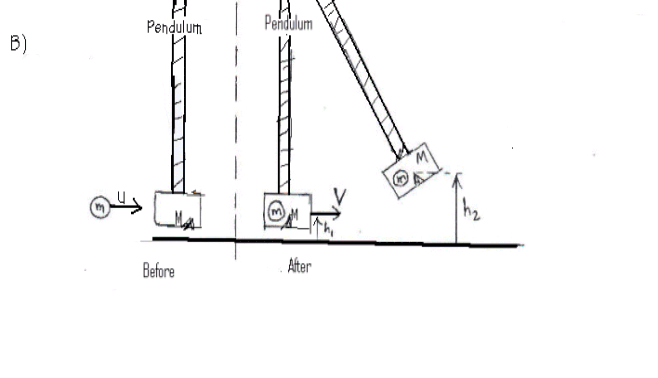
The collision is completely inelastic. The momentum is conserved but the kinetic energy is not conserved. After the collision the energy is conserved. Just after the collision the pendulum & ball has kinetic energy and it is converted into gravitational potential energy when the pendulum & ball is raised to a height. After the collision, use the conservation of energy, and derive an expression for V.

Use the conservation of momentum for the collision, and derive an expression for u.

Procedure:

A) Measurement of the range and fall of a projectile.

1) Support the pendulum on the pawl and get the gun ready for firing.

2) The ball is fired horizontally to hit the floor. Fire the ball and determine approximately where it strikes the floor. Place a sheet of white paper on the floor so that the ball will hit it and secure the white paper to the floor with some tape. Place a carbon paper over the white paper. Fire the ball 4 more times.

3) Measure the range X and the vertical distance of fall, Y as shown in the diagram and complete the data table.

B) Ballistic pendulum

4) Get the gun ready for tiring. Allow the pendulum to hang freely. When the pendulum is at rest, fire the ball into the pendulum bob. Record the notch number on the scale reached by the pawl when it catches the pendulum. Remove the ball from the pendulum.

5) Repeat procedure (4) 4 more times.

6) Compute the average value of the notch number. Set the pendulum with the pawl engaged in the average notch number, measure the height h₂ from the base of the apparatus to the index point on the pendulum.

7) With the pendulum hanging in its lowest position, measure the height h₁, from the base of the apparatus to the index point.

8) Record the mass of the pendulum, measure the mass of the ball, and complete the data table.

DATA TABLE:

A. Determination of the initial velocity (u) of a projectile from range and fall measurements:

Vertical distance of fall = Y = ________________________

Time of flight = t = __________________________

Average range = X =________________________

Initial velocity = u =__________________________

B. Determination of the initial velocity (u) of a projectile using ballistic pendulum mehtod.

Average notch # =__________________

Height h₂ of pointer with

pendulum catch in average notch number =_________________________

Height h₁ of pointer withpendulum freely suspended =__________________

mass of ball                             m = ____________

mass of pendulum                   M= ______________

Velocity of the pendulum & ball just after collision = V = ____________________

Initial velocity                        u = ________________

% difference between results of parts A and B = ____________

Use your data for part (B), in SI units, to answer the following questions.

1) Calculate the kinetic energy of the ball before the collision.

2) Calculate the kinetic energy of the ball and the pendulum bob just after the collision.

3) Calculate the energy loss due to the collision.

4) What fraction of the initial kinetic energy is lost?

5) What happened to the lost energy?

6) Show that the fractional loss of energy is also given by the ratio M/(m + M), where M - mass of the pendulum, m - mass of the ball. Calculate this ratio and compare it with the results from (4) above.

Conclusion: