Name:_______________________________Date:_______________Time:____________

Partner(s):_____________________            Course:_________________

________________________________________________________________________

Uniform Circular Motion

Purpose: To determine the centripetal force required to keep a known mass at a uniform circular motion.

Apparatus: Centripetal force apparatus, stop clock, meter stick, knife-edge stand, knife-edge clamp, mass-set, and mass-hanger.

Theory: a. Circular Motion

In this experiment a body of mass, m, is made to rotate in a circular motion. The speed of the revolving body will be (or should be) kept constant. Even then there is acceleration because the velocity changes direction continuously. The acceleration is called centripetal (or center seeking) and is given by:

a_c =  v² / R ; where v is the linear speed of the revolving body and R is the radius of the circle of revolution.

Using Newton's second law the centripetal force can be written as:

F_c =  m v² / R ; where m is the mass of the revolving  body.

The linear speed  v can be measured using the following equation:

b. Measuring the mass of the revolving body, unknown mass, M1:

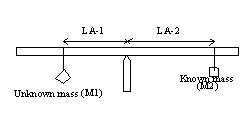
This mass is too heavy for the electronic balance. A beam-balance method will be used to measure its mass. Meter stick is supported at the center of gravity.

Unknown mass will try to rotate the meter stick counter

clockwise and known mass will try to rotate the meter stick clockwise.                                           

Counter clockwise torque = Unknown mass X Lever-Arm-1

Clockwise torque = Known mass X Lever-Arm-2

For balance, counter clockwise torque must equals the clockwise torque.

Unknown mass X Lever-Arm-1 = Known mass X Lever-Arm-2

Unknown mass = [Known mass X Lever-Arm-2] ÷ [Lever-Arm-1]

Procedure:

1) Clamp the meter stick in the support clamp at its center of gravity. Hang the unknown mass near one end of the stick. Hang a 400 gm mass near the other end of the stick and obtain the balance. Record the positions of the masses. Determine the Lever-Arm-1 and Lever-Arm-2 and finally the mass of the revolving body.

2) Level the apparatus with the adjusting screws provided for that purpose. The apparatus is level when the crossbar will stay in any arbitrary position.

3) Set the radius indicator for minimum radius, then set the crossbar so that the body (mass m), with spring unattached, hangs directly above the radius indicator. Measure and record this radius in the data table.

4) Now attach the spring to the body and determine the static force necessary to return the body to a position directly above the radius indicator. Record the mass, m_s, in the data table.

5) Disconnect the hanging mass from the rotatable mass and practice rotating the crossbar by hand, using the finger grip provided, until you are proficient at maintaining a frequency of rotation that will keep the rotating mass at the radius of the indicator.

6) Measure the time required for a definite number rotations (at least 50) of the crossbar.

7) Repeat procedures 3 - 6 for other values of R, ending with the maximum possible value.

DATA

A. Mass of the revolving body, m.

Draw a diagram of the balanced meter-stick in the box below and record the positions for center of gravity, unknown mass, and known mass.

Known-mass = ________________

Lever-Arm-1 = _________________

Lever-Arm-2 = _________________

Unknown-mass = m = ____________

Use SI units:    Mass of the revolving body from above, m = ___________

8) Enter the above data in a spread sheet program and calculate the following:

mass of the rotating body = m = _____________

10) Compare the mass from procedure (9) with that from procedure (1).

11) Observe your data and explain why the total time decreased as the radius increased?