PHYS 202l Capacitor Lab Name:____________________

A. Purpose: To investigate various combinations of capacitors.  

Apparatus: Three capacitors, digital multimeter, and banana plug wires.

Theory:

When two or more capacitors are connected in series the equivalent capacitance, C_S is given by;

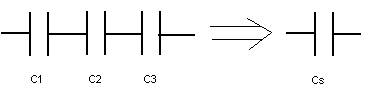
When two or more capacitors are connected in parallel the equivalent capacitance, C_P is given by;

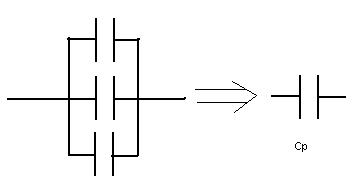
Procedure:
1. Measure the values of the three capacitors using the digital multimeter (DMM) and record them in the data table.
2. Connect the three capacitors in various combinations and sketch the combination diagram. Also, measure and calculate the equivalent capacitances.
3. After completing the data table, identify the highest capacitance and the lowest capacitance in the data table.

DATA: Measured values: C₁= _______       C₂ = _______    C₃ =__________

Capacitor Combination Diagram	Capacitance Values
	Measured	Calculated
All three in series
All three in parallel
1 and 2 in parallel and 3 in seies.
1 and 2 in seires and 3 in parallel with two  of them.

Identify the highest capacitance and the lowest capacitance in the data table, above.

B. Purpose: Investigate the discharge characteristics of a capacitor.

Apparatus: PC with Pasco 750 interface, capacitor, power supply, alligator clips (2), voltage sensor, decade resistance box, light bulb, knife-switch, and connecting wires (4).

Theory: The capacitance (C) of a capacitor is given by, where Q is the charge stored and V is the potential difference.

The charge stored is equal to the product of current and time, which can also be determined by finding the area under the Current versus Time graph.

http://hyperphysics.phy-astr.gsu.edu/hbase/electric/capdis.html

Procedure:

1. Plug in the power supply and set the voltage to 5 volt.

2. Set up the following circuit, which will be used to charge and discharge the capacitor. Have the circuit checked by instructor.

3. Set R = 10 ohm, while the knife-switch is open, plug in the black banana plug to fully charge the capacitor, for about 3 minutes.

4. Setting up the Interface:
a. Make sure that the power for the interface is turned on.
b. Plug in the voltage to analog input A on the interface.
c. Open PASCO Capstone software from the desktop.
d. Click Hardware Setup under Tools on the left, click on the interface input where the sensor is connected and select Voltage Sensor. Click Hardware Setup again to close it.
e. Double-Click Graph under Displays on the right, click Select Measurement, and select Voltage (V).
f. Click Record, un-plug the black banana plug, and close the knife-switch to discharge the capacitor through the 10-ohm resistor in the decade resistance box.

5. Continue collecting data until the capacitor is completely discharged, as shown below, for about 2 minutes.

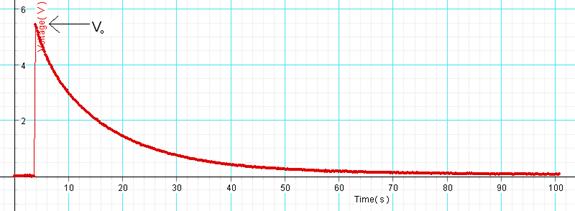
6. Stop the data collection, and determine the maximum voltage (V₀) using the Show coordinates tool.

7. Find the area under the curve, using the Display area under active data tool, 6^th from left.

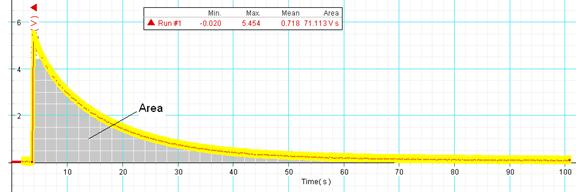
8. High-light the discharging portion of the graph, fit it with a natural exponent function, and obtain the time constant from the fit.

9. Repeat the measurements for other R values and complete the data table.

DATA:

R (Ω)	V0	Area under Voltage vs. Time	Total charge, Q0*	Capacitance,	Time Constant** using R & C values	Time Constant from fit***
10
20
30
40
50

*Total charge, Q₀ is equal to the Area under Current vs. Time, which is obtained by dividing the Area under Voltage vs. Time by the resistance, R. Explain why?

________________________________________________________________________

________________________________________________________________________

** Time constant = RC.

***In terms of the exponent coefficient ‘B’ of the Natural Exponent Fit, the time constant, RC is given by:

Conclusion: